IBL原理 : 基于物理的光照:环境光照 (Enviroment Lighting)(1)
Unity 处理IBL主要是通过 GlossyEnvironmentReflection 这个函数来处理IBL的。
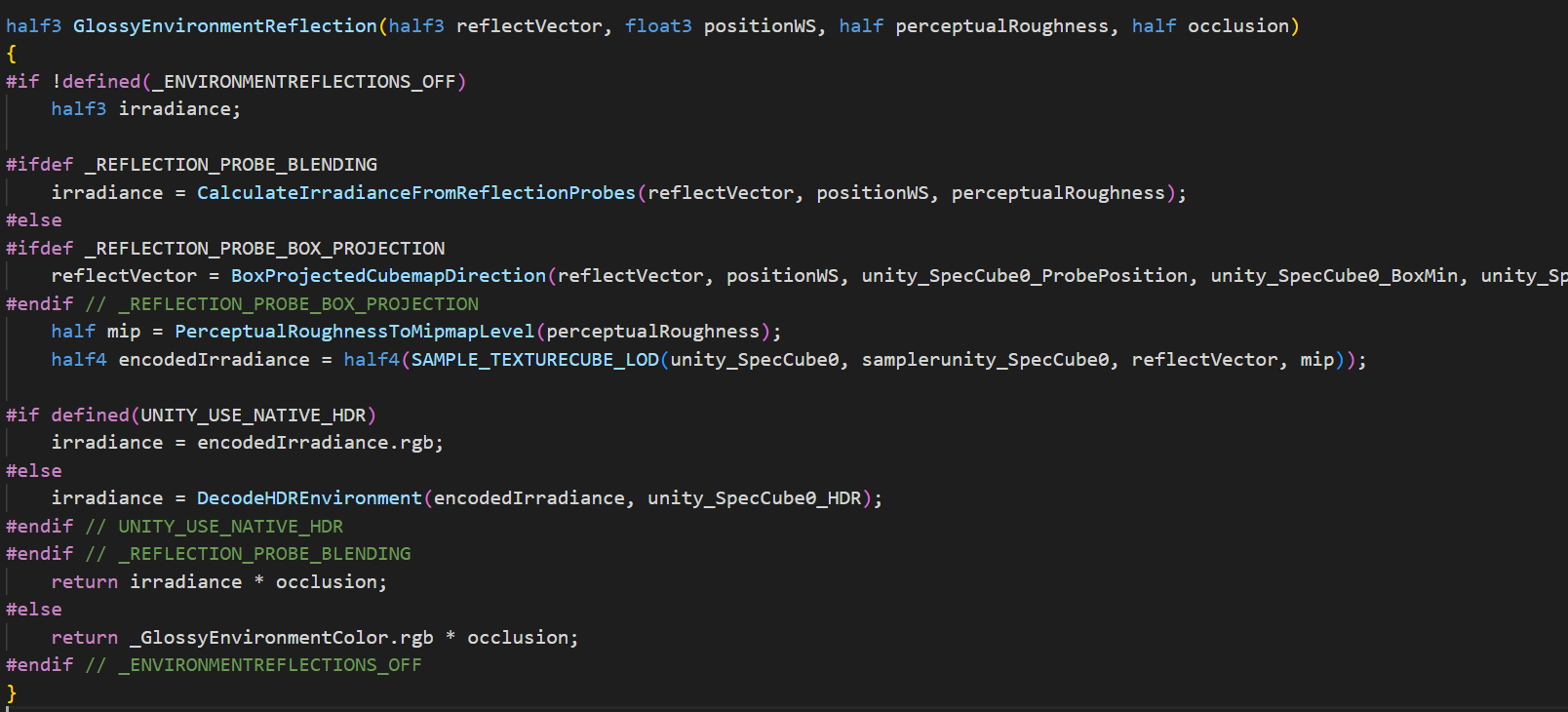
其中通过PerceptualRoughnessToMipmapLevel 来获得环境图的mip的层级:
PerceptualRoughnessToMipmapLevel 方法背后的数学和原理
Unity提供了两种在IBL中将Roughness映射到MipmapLevel的方法,想必大家第一眼看上去会很困惑。这里我先贴出两种
方法源码:
A版本:
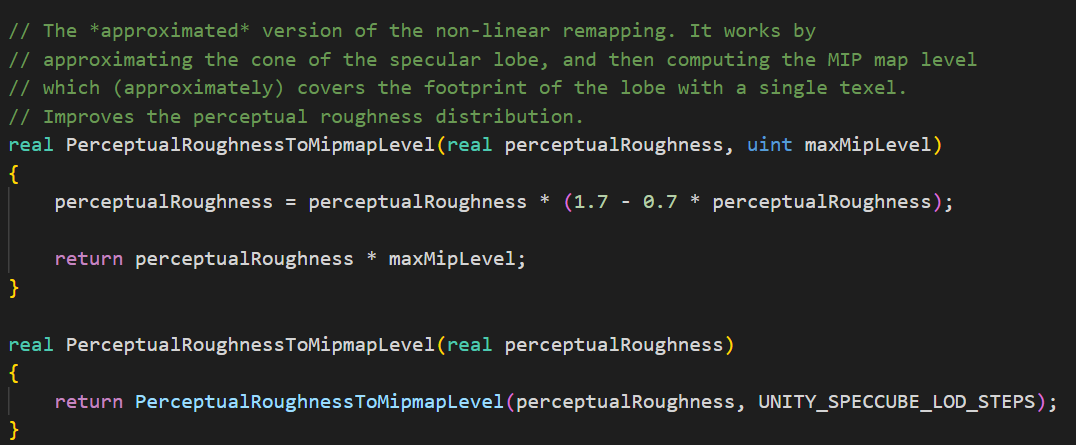
B版本:
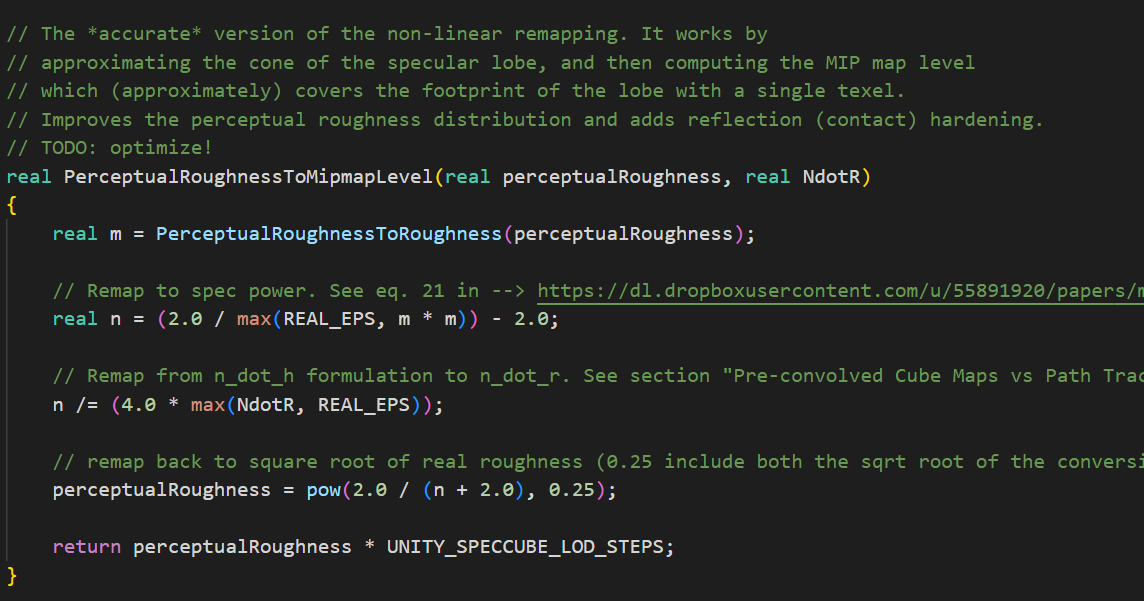
首先A是B的简化近似版本,这点我帮大家做了个表格
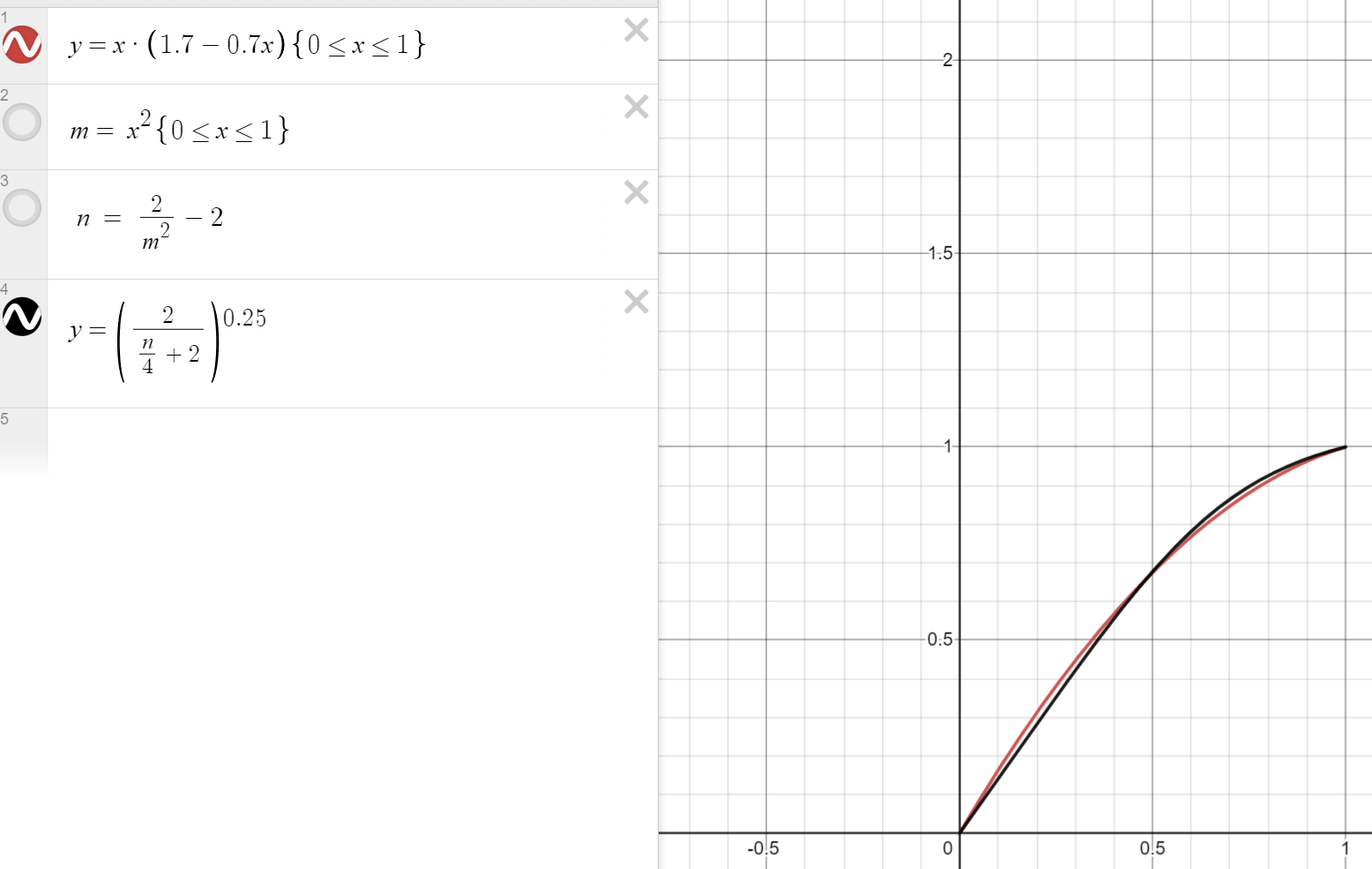
那么B代码是什么含义呢?
吐槽:当你访问注释的这个网址的时候:https://dl.dropboxusercontent.com/u/55891920/papers/mm_brdf.pdf,会给你一个大大的404。Unity官方是真的懒,也不更新一下。
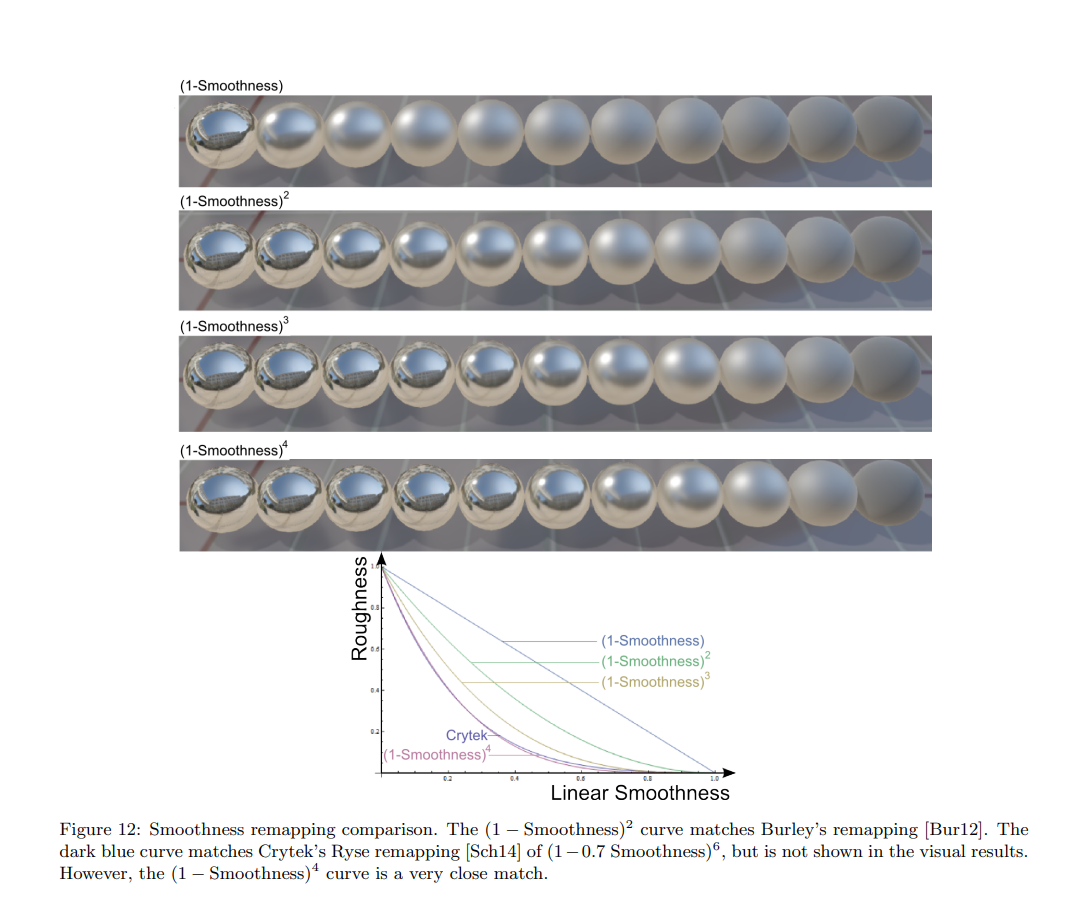
实际上,我们人眼感知的Roughness和实际世界中的Roughness并不一样(类似于线性空间工作流和gamma工作流),为了方便艺术家在引擎中引入了PerceptualRoughness(实际上Unity中艺术家直接接触的是更容易理解的smoothness,smoothness = 1 - Roughness,而引擎里计算的是Roughness,不影响上面的结论,大家明白就好)。Roughness和PerceptualRoughness实际上是一个平方根的关系,并不是线性的。
我觉得寒霜PBR的PDF(见PBR专栏导言附录)中这部分解释的很好(至于Unity的我没找到,也可能是根本没有):


最直观的还是PDF中下面这个图,这里就做了一个映射关系。大家联想下线性空间灰度值那张pow2.2的图就能很轻松的明白了:
所以B函数实际上就是Unity引擎里一个从实际roughness到艺术家用的roughness的一个映射函数(用smoothness一样的)
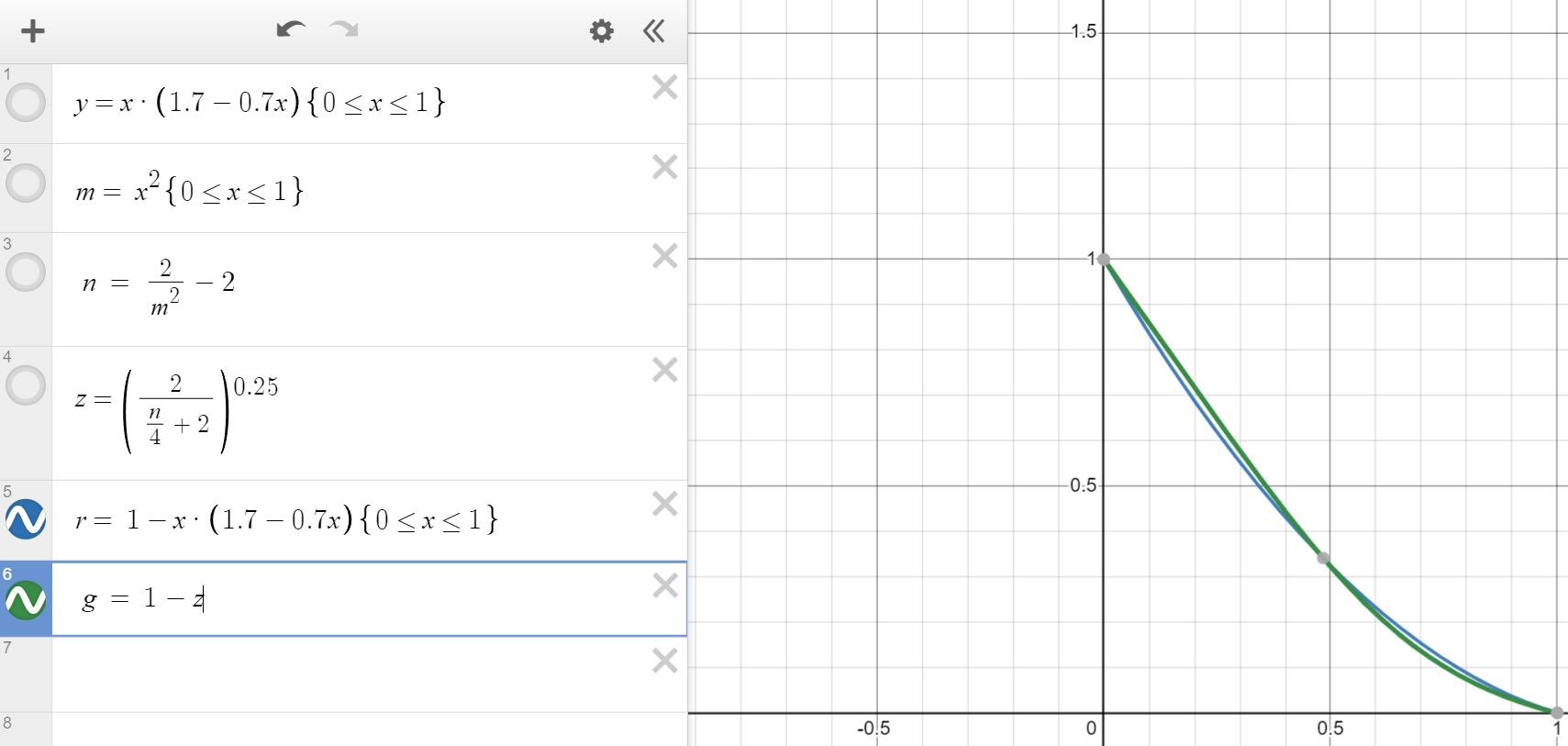
OK,B这部分解决了。那还有B中的这个REAL_EPS到底是啥作用呢?
这个东西一眼让我想到了几年前写games101光线追踪部分时遇到的一个问题,浮点数溢出,当时我用__FLT_EPSILON__解决了这个问题并分享到了GAMES论坛上(太久远找不到了),但是csdn中我的旧博客还在(不用关注了,csdn已经弃更了),有兴趣的小伙伴可以看一下原文。


这个问题很难遇到但是是实际引擎里会遇到的。更详细的解释可以看下这位博主的博客。
此外 UNITY_SPECCUBE_LOD_STEPS 是Spec Cube Mipmap最后层级,对应的是6。如果你改用了别的spec cube,建议最大index不要太高,用6也是可以的。