这里结合一下GAMES101和GAMES202讲一讲渲染方程的由来。虽然Bounding Volumes这些加速结构和渲染方程没有直接关系，但是由射线方程和辐射度量学构成了渲染方程的基础。

射线方程

首先是射线方程，我们根据射线的起始点和方向来定义一条射线

渲染方程（1）射线方程和Bounding Volumes-tajourney

射线有一个小作用就是能判断一个点是否在一个封闭的几何体内部：

从此点向任意方向发射一条射线，如果求得的交点的个数为奇数，则在内部；否则就在外部。

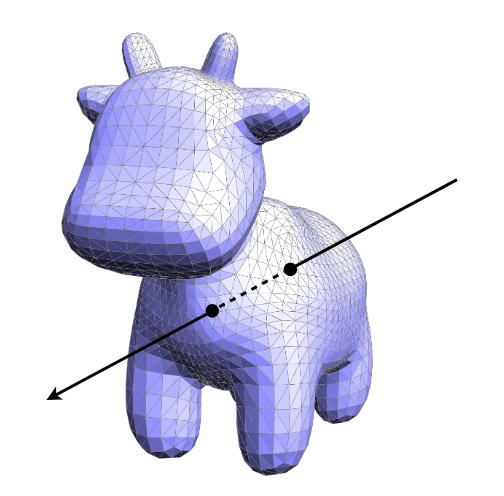
渲染方程（1）射线方程和Bounding Volumes-tajourney

射线与三角形求交

我们可以把一条射线与三角面求交这个问题拆分为两步：

1.射线与三角面所在的平面求交

2.根据1得到的交点，判断此交点是否在三角形内部

如何定义一个平面？我们可以用一条法线和一个平面上的点来定义：

渲染方程（1）射线方程和Bounding Volumes-tajourney

此外还有MT算法

渲染方程（1）射线方程和Bounding Volumes-tajourney

关于第二步，我们可以用重心坐标或者叉乘或者面积法来求，下面是二维空间重心坐标一个示例。

// 重心坐标 (α, β, γ)，(x1,y1)(x2,y2)(x3,y3)是三角形三个顶点，(x,y)是任意一个点
let alpha =  ( ((y2 - y3)*(x - x3) + (x3 - x2)*(y - y3) ) / 
              ((y2 - y3)*(x1 - x3) + (x3 - x2)*(y1 - y3)) );
let beta =   ( ((y3 - y1)*(x - x3) + (x1 - x3)*(y - y3) ) /
              ((y2 - y3)*(x1 - x3) + (x3 - x2)*(y1 - y3)) );
let gamma =  1.0 - alpha - beta; 

//如果求得的α, β, γ均>0且<1，而且α+β+γ=1，则点在三角形内部

叉乘就更好求了，用三条边的向量和点到三个顶点的向量分别做叉乘，同号则在内部，否则则在外部。

面积法就是求点和三个点构成的三个小三角形的面积和，等于就在内部，否则就在外部，不过此方法并不常用。

Bounding Volumes

AABB(Axis-Aligned Bounding Box)轴对齐包围盒

对于一个AABB，我们可以求得光线和每个对面相交的时间的集合，从而：

t_enter = max{t_min}
t_exit = min{t_max}

对于射线来说：

渲染方程（1）射线方程和Bounding Volumes-tajourney