最近在自己的SRP里重写PCF算法及采样优化思路,就想参考一下Unity本身是怎么实现的,看了下Unity的源码实现方式和备注一脸雾水。查阅资料也只发现了https://blog.csdn.net/cgy56191948/article/details/105726682/ 这篇文章中提到过算法实现,但是对于算法优化的实现原因并没有解释。我写文章或者工程的过程中不把每个细节的实现及思路给摸清楚就不舒服 = =,便停下手来专心找资料。昨日逛知乎偶然看到z大的pcf文章https://zhuanlan.zhihu.com/p/369761748,竟然和我前面的经历一模一样。。看完他文章之后茅塞顿开,并且和z大交流了很多,非常感谢z大的帮助。排坑之后我决定整理并分享一下自己的学习笔记和学习过程,大学期间学习的数字图像处理的知识都快忘完了~。而且网上关于Unity PCF优化采样的算法的分享实在实在是太少了。
PCF本身思路是非常简单,比如AK佬这篇https://zhuanlan.zhihu.com/p/462371147就是原始的PCF采样(用的泊松采样实现的优化,但是效果是不如Unity默认的),如果采用原有采样思路,Shader内部也非常好实现。但是如此暴力的算法闫老师也说了代价非常昂贵,现代引擎中如果采用pcf肯定对pcf采样进行了少不了优化。
那么Unity是怎么优化PCF的采样插值计算的呢?
正文
1.pcf原始的采样算法
这里可能需要一点点数字图像处理的知识,之前没有学习过的也不要慌张,我会慢慢的讲。
图像上的纹素点实际上是一个个离散的点,如果把采样得到的值(假设采样后得到的是灰度值)以一个一维图像来表达如下:

在上诉条件下,当我们使用point进行采样(最近邻算法)的时候,实际上相当于利用box-filter进行采样,当前像素的都会取用最近的采样点的值,如下:

而为了让图像看起来不那么糟糕,我们一般采用双线性插值技术,也就是下图中的bilinear
这里借用一下闫老师的ppt:

把bilinear放到信号处理中,实际上就是用Tent Filter进行线性插值如图下,假如x是我的任意一个一维坐标上的值,当x位于两个采样点中间时,显然x的采样值是这两个采样点线性插值得到的:

上文可以推广到任意一个图像采样,采样阴影对比后的结果也是如此,这也是pcf常规的采样插值做法。
2.PCF的采样算法优化思路
如果你直接看Unity ShadowSamplingTent.hlsl这个源文件,可能会云里雾里的。所以我从优化的原因讲起。
这里直接引用@zilch的结论和图片:

使用传统的插值,在阴影渐变之间似乎存在一些明显的边界,像是一块块似的。为什么会这样呢?
用一纬的示意图来表示就是:
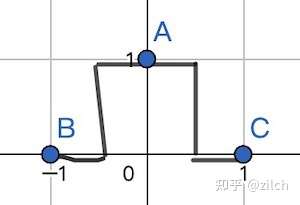
本质原因是,线性插值是仅仅一阶连续的,其导数是不连续的。
ABC的点本来是离散的取值,在进行线性插值后会变成如下图:
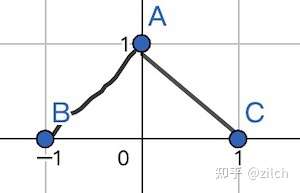
可知,导数在A点是不连续的,带来的效果就是A点很尖锐,于是形成了鲜明的分界线。
更进一步的分析,Bilinear Interpolation本质上是一个离散的Tent Filter。 之所以会造成这种尖锐,正是因为Filter是离散的,它将像素看成了点,只计算了那个点的权重,而不是计算像素整个面积所占据的权重。
很多网上的文章都使用了这种采样方式去扩大PCF的核,但其实效果很不好,而且N * N的核需要进行(N-1) * (N-1)次采样,是Performance Killer。
也就说,如下图所示:假设D是我实际的像素点的某一段一维坐标,A、B、C都是对应的贴图上的纹素的一维坐标,那么我拿到的对应的像素点的D值如下图:

实际上得到的结果是离散的Tent Filter,那该怎么才能做到连续的Tent Filter呢?答案就是:考虑面积,做卷积,也就说求特定区间的积分!
这恰巧和Z大的思路一致,再次引用一下他的原文思路:


这里我梳理一下整个流程:

分段函数g_shadow(x)是使用f_w(x)对f_shaodw(x)做卷积,这个分段函数我推导了一下并不难,为了方便大家理解,我画了一下当x<0时和-1.5<x<0时的图,以几何的方式来说明(阴影区域就是>0部分的面积):


同理可推出x>1.5,0<x<1.5的情况。
再次引用一下z大的结论:

3.PCF优化采样算法应用思路
在硬件中我们会使用SampleCmp采样临近的4个像素位置(在Unity中具体怎么实现的可以参考我的另一篇讲GAMES202作业1的博客http://tajourney.games/5413/或者z大的原文章)。也就是说,以一个PCF NxN为例,需要采样中间(N-1)^2个采样点。
以PCF4X4为例,如果不采用优化思路,那么总共需要采样3x3=9次,但是沿用上文PCF优化的策略,采用面积的覆盖权重代替采样点的权重,既能优化阴影质量,同时还能降低采样次数为(N/2) ^2,也就是说PCF4X4仅需采样4次即可。


这样,我们就能分别计算出每个像素(texel)的权重。
4.Unity PCF Tent采样算法实现
这一部分是Z大原文章并未提到的,所以我会重点讲下并复算一下Unity的思路。
我们看一看Unity的算法到底是怎么实现上文思路的:

这部分很简单,初高中的几何知识:

有了上文的思路,我们知道对于一个等腰直角三角形(以上图右半部分为例),它第一个纹素(texel)对应的面积(阴影部分)就是,注意,这里以及后面的texel实际上指的是某一方向上分布的texel,比如U方向或者V方向(高为2个texel),并不是单个的texel,原因如上面所说,硬件的采样规则为每次采样周围2X2:
S = (h + (h-1))*1/2 = h - 0.5那我们要求出4部分texel的面积以及面积的权重w1、w2、w3、w4呢?以3*3大小的filter为例
求面积:


如上图:设offset为x,那么显然:
w1 (对应computedArea.x) = (-x+0.5)* (-x+0.5)* 0.5 = (x+0.5)* (x+0.5)* 0.5 - x
w4(对应computedArea.w)= (x+0.5)* (x+0.5)* 0.5
而w3相当于边为 1.5+x的等腰直角三角形落在第一个像素上的面积S(即上文的SampleShadow_GetTriangleTexelArea方法)减去左上角的三角形面积S1

w3(对应computedArea.y)
= SampleShadow_GetTriangleTexelArea(1.5 + x ) - (max(x,0))^2 * 0.5 * 2
= SampleShadow_GetTriangleTexelArea(1.5 + x ) - (max(x,0))^2
同理得
w2 = SampleShadow_GetTriangleTexelArea(1.5 - x ) - (min(x,0))^2
求面积权重: Weight/S (上上小节已经算过,面积是9/4)= Weight * 0.44444

至此,我们得到了根据Offset值推出w1-w4,4个texel的权重值。
再之后,我们需要上文中提到的求P1-P4坐标(位置),并分别处理横纵轴上的权重。来看看Unity是如何处理的:

输入数据是SM大小和对应采样点的UV值(ps:URP/SRP 里real就是会根据平台选择为float或者half)
//把纹理映射坐标(UV)转为纹素坐标,_ShadowMapTexture_TexelSize.zw为阴影贴图的长和宽方向各自的纹素个数
float2 tentCenterInTexelSpace = coord.xy * _ShadowMapTexture_TexelSize.zw;
//floor 函数向下取整,得到纹素的Index
float2 centerOfFetchesInTexelSpace = floor(tentCenterInTexelSpace + 0.5);
//计算tent中点到fetch点中点的偏移值(即上文中P1-P4到中心点P的偏移)
float2 offsetFromTentCenterToCenterOfFetches = tentCenterInTexelSpace - centerOfFetchesInTexelSpace;
//有了偏移,我们就可以套用上文SampleShadow_GetTexelWeights_Tent_3x3来求权重
//...
//求出每一块面积(fetch)的权重。举例:如果是平均分开了4块区域,那么fetchesWeightsU就是(0.5,0.5),fetchesWeightsV就是(0.5,0.5),也就是说每个fetch的权重是相邻texel的权重和。
//fetchesWeightsU.x = texelsWeightsU.x + texelsWeightsU.y;
real2 fetchesWeightsU = texelsWeightsU.xz + texelsWeightsU.yw;
real2 fetchesWeightsV = texelsWeightsV.xz + texelsWeightsV.yw;
//求每一块对应的阴影权重,根据双线性插值的公式反推出fetch的位置
//move the PCF bilinear fetches to respect texels weights(原始的插值是按2x2来算的)
real2 fetchesOffsetsU = texelsWeightsU.yw / fetchesWeightsU.xy + real2(-1.5,0.5);
real2 fetchesOffsetsV = texelsWeightsV.yw / fetchesWeightsV.xy + real2(-1.5,0.5);
fetchesOffsetsU *= shadowMapTexture_TexelSize.xx;
fetchesOffsetsV *= shadowMapTexture_TexelSize.yy;
real2 bilinearFetchOrigin = centerOfFetchesInTexelSpace * shadowMapTexture_TexelSize.xy;
fetchesUV[0] = bilinearFetchOrigin + real2(fetchesOffsetsU.x, fetchesOffsetsV.x);
fetchesUV[1] = bilinearFetchOrigin + real2(fetchesOffsetsU.y, fetchesOffsetsV.x);
fetchesUV[2] = bilinearFetchOrigin + real2(fetchesOffsetsU.x, fetchesOffsetsV.y);
fetchesUV[3] = bilinearFetchOrigin + real2(fetchesOffsetsU.y, fetchesOffsetsV.y);
fetchesWeights[0] = fetchesWeightsU.x * fetchesWeightsV.x;
fetchesWeights[1] = fetchesWeightsU.y * fetchesWeightsV.x;
fetchesWeights[2] = fetchesWeightsU.x * fetchesWeightsV.y;
fetchesWeights[3] = fetchesWeightsU.y * fetchesWeightsV.y;这里补充解释下求每一块对应的阴影权重,根据双线性插值的公式反推出fetch的位置这句话。
我们知道像素双线性插值的公式是:
假设 两个间距单位像素的点 X坐标分别为X1,X2,权重值为W1,W2,则插值后的点X为
X = W1/(W1+W2) * X1 + W2/(W1+W2) * X2
这里 Offset = W2/(W1+W2)
即 Offset = texelsWeightsU.y / (texelsWeightsU.x + texelsWeightsU.y) //求出相对的偏移值
如果算上坐标到fetch的实际的偏移,还要加上(-1.5,0.5)
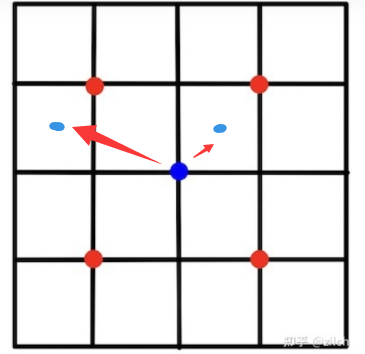
Y同理。所以Unity这里会
real2 fetchesOffsetsU = texelsWeightsU.yw / fetchesWeightsU.xy + real2(-1.5,0.5);
//等价于:
fetchesOffsetsU.x = texelsWeightsU.y / (texelsWeightsU.x + texelsWeightsU.y) - 1.5后面无非是一些filter区域大小上的差别,就不再赘述了。
总结
这次学习重拾了大学不少东西,收益很多(这里也推荐一下大学的学习教材《数字图像处理》(冈萨雷斯),讲的非常好,目前应该是第四版了)。在最后再次感谢z大的帮助。事后我去评论区看了下相关的paper( 在书的第一篇 《fast conventional shadow filtering》),确实也有相关的减少采样次数的优化思路。
这里附上相关pdf:
为啥tent filter的值要和三角形的底的一半相同呢?filter的值大于1这块儿一直云里雾里,我的直觉告诉我这样会放大原本的信号数值,可能我需要学习一下信号处理的知识了吧。。头大
@Llugaes: 因为采样图像(UV)的时候是一样的呀
@糯米: 完蛋了,你的回答和我掌握的知识没法自洽,我没学过信号处理,对卷积的认知也仅限于shift、mul、sum,所以我理解这个问题的角度就像是对每个像素中心点采样出来的值用filter从左往右过一遍,但是这样的思考角度带入到3x3的tent filter的案例中就完全昏厥了,我只能get到从离散卷积改为连续卷积,但是这个纵坐标的value值给我整蒙了,进入了自己钻自己牛角尖模式哈哈哈哈(无奈
@Llugaes: 你可以理解每个采样点的间距是相同的,所以肯定是等腰直角三角形
@糯米: 左思右想没能对上频道,感觉十分羞愧。但是我换了一种角度,因为是linear所以要满足x函数并且过左右两个N/2的点,所以因为是ax+b,a为1,所以一定会是等腰直角。但是这样的话就没法理解作为滤波时的思考角度了。。越来越觉得我没有思考在对的方向。像大佬说的,采样间距相同,但是我理解这句话感觉好像是从1D转换到2D的角度理解了,但是这里的滤波不是在分析1D的情况嘛,这也是困扰我的一个点。。我还是回炉重造吧orz
@Llugaes: 把二维拆分为一维这里只是简化方便分析,因为uv两个方向任意一个都是相同的一维,从数学的角度分析你会越想越复杂,从图像的采样点来考虑
@糯米: 我再思考思考,话说大佬加个联系方式呀,在知乎私信你好像没注意到hhhh
@Llugaes: 哈哈哈,知乎最近两天没看,不好意思
按我自己的理解,本质上还是因为Texel是离散的信号,从而使阴影边界看起来有突变。假设Texel趋近无限,继续使用Tent filter,能够从视觉上消除边界,但其实从数学上来说,应该依然是存在“边界”的,因为双线性插值本身就是线性的,一阶导之后,在相邻两个信号处必然会产生跳变。或者就是像文中一样使用面积来作为Tent Filter,因为此时Tent Filter已经不是一阶的了,一阶导之后不会出现跳变,反应到原始图像上就是双线性插值的阴影边界的拐点理论上被平滑
@1684991993735: 好理解
半年后又重新更新了一下文章,补充了一些细节
一年前这篇文章的公式部分当时没用latex数学编辑器,排版可能有些丑,请见谅233
请问,根据面积对tent filter进行优化的这个方案,和bicubic多项式插值有什么区别吗
因为bicubic构造的函数也是16采样点采样,而tent filter这里做积分,从结果上看也提高了多项式的次数
另外从频域角度看,tent filter相当于两次最近邻插值,也就是两次box filter(两次门函数的卷积,根据卷积的结合律,可以使用门函数对门函数先行卷积,结果等于三角脉冲,和tent filter等价),而双三次插值就是三次box filter,那么这里这种根据面积的filter优化,从信号角度应该如何理解呢
@1697112270663: tent filter相比shader中只需要采样4次哈(按你提到的4x4的TentFilter, 采样次数= (4-2)^2 = 4),剩下的是利用硬件pcf每次2x2 block,并不是16个采样点,只是采样的区域相同。bicubic是直接考虑周围像素的权重吧
@1697112270663: 是的没错,4x4的TentFilter之所以只要在shader里采样4次,还是因为硬件帮忙做了双线性滤波,如果没有硬件的双线性采样,体现在shader里就和bicubic无异。而3×3的tentfilter,一方面,从面积这个角度,有点不太明白你推导过程中的卷积是在对什么卷,另一方面,双线性滤波常常伴随着采样率的变化,也即离散卷积,3×3的filter不符合金字塔,就有点反直觉。
所以我对z大和你这里提出的这种加权方式的理解,大概是属于bilinear到bicubic的折中,也正因这一点多项式系数才会出现分数。如果只是对伪影感到不满的话,这种方法应该无法实质上解决问题,就算是bicubic也会引入一定的振铃效应,仅仅做到了高阶导连续而并未在高频信号滤除方面体现出特别的优势。但在这个问题上继续深入又回到了模糊算法那边,高斯kawase blabla,对一个阴影如此钻牛角尖属实有点难评
@Yui Lu: 实际上我也不是对PCF的这个做法存在什么疑问,我本身找到这个帖子是从dual blur那过来的,是关于升降采样与滤波的先后顺序(信号角度),以及部分资料所说的硬件插值减少计算量的一些疑问(起点是AK佬的Bloom:https://zhuanlan.zhihu.com/p/525500877)
我也没想到我会在这个问题上越钻越深,在网上转了好几圈都没找到几篇像你这样从信号角度提供理解的文章,所以如果可以的话,能不能加个联系方式再请教一些别的问题呢(个人也没系统学过信号处理,也只是到冈萨雷斯书上那点内容,所以上面发的也有可能有些理解不到位orz)
@Yui Lu: q1063738783,工作时间并不一定能及时回复哈
@Yui Lu: 逐个回答你的问题:
1.体现在shader里就和bicubic无异:这句结论并不正确,权重算法并不一样
2.对什么卷积:采样值(阴影强度),算面积是为了推导各个texel对应的权重
3.多少大小的filter对Tent这个算法本身没有影响,可以先看下Unity的源码,最后都会走SampleShadow_GetTexelAreas_Tent_3x3
4.关于采样为什么会走样可以重新看下games101,采样本身就会丢失信息,Unity tentfilter这个算法所做的工作目的是解决采样本身的问题,而非解决采样后的值的问题
5.pcf ≠ 模糊。至于什么样的算法更优势这些,本篇文章只是解析Unity为什么这么做,有做的更好的PCF采样算法可以分享
@糯米: re1:权重算法是不一样,但本质上做的事情和bicubic没啥差别了吧,pcf其实一开始也是抗锯齿算法,这点上是通的
re3:确实没影响,实际上pcss的filter size直接就是自适应的hh,所以我主要的点不在pcf
re4:丢失信息没问题,但造成走样的根本在于信号的混叠,在于采样的离散化带来频域周期化的这个过程
另外这个q好像查无此人hhh,要不大佬加下我?2903077287
@Yui Lu: 我搜了下自己确实搜不到,貌似是设置的问题。